P1721 [NOI2016] 国王饮水记 题解
题意简述
给定 个城市,第 个城市收集到了高度为 的水,要求通过使用
次地下连通系统,每次使用可以使若干个城市的水箱相连通,然后使它们的水位变为它们的平均值。要求求出
次操作后, 号城市水箱中的水位的最大值。
策略选择及最优性证明
引理0:我们一定不会对初始水位不高于
号的水箱操作,操作与操作之间选择的水箱一定不会有重叠。
证明:显然。
引理1:对于初始水位高于
号的所有水箱,我们应当从小到大进行操作。
证明:对于两次操作,不妨设其中一个选择是 个水箱,它们的值分别为 ;另一个选择是 个水箱,它们的值分别为 。设操作前 号水箱的水位为 ,且根据引理1,数组
中的任意数比 中任意数小。那么,如果先选择操作 ,
号水箱的水位会变成:
否则, 号水箱的水位会变成:
作差可得:
由此证毕。
引理2:如果我们需要在水箱集合 中选择 个水箱进行一次操作,那么选择水位最高的
个一定是最优的。
证明:设操作前 号水箱的水位为 ,选择的水箱水位分别为 。那么,操作后的水位可以表示为
。显然,我们希望操作后水位尽可能大,只需要让 最大即可,也就是选择最大的 个。
根据引理1以及引理2,我们可以从小到大进行dp,如下是一个显然的dp转移方程:
状态 代表前 个水箱中已经操作过 次后 号水箱中的最高水位, 代表前
个水箱初始水位的前缀和。注意到转移可以压掉一维,忽略掉
一项(过程中直接继承即可),方程转化成:
至此,我们就找到了
的初步算法。(关于为什么复杂度里面没有 ,我们可以在
时存一下是从哪个状态转移过来的,过程中不必使用高精类,最后时再进行一遍深搜统计最终答案就好了。)
算法优化
基本尝试
然后应该做什么呢?
观察转移方程,经过初步尝试后,可以发现这个式子难以进行常规的斜率优化,甚至可以说是不可能,因为交叉相乘后出现了类似于
的二次项。(@OvO_Zuo
:不然你猜它为什么是黑的)那么,我们就需要另辟蹊径。
另类斜率优化
注意到转移方程中的式子其实本身就是一个斜率式子。设两个点 和 。原式恰为第二个点关于第一个点的斜率。接下来,让我们分析这种特殊的斜率的性质。首先注意到原式一定是正的,即斜率一定是正的;另外, 一定比 要大。同时, 和 都是单调递增的。
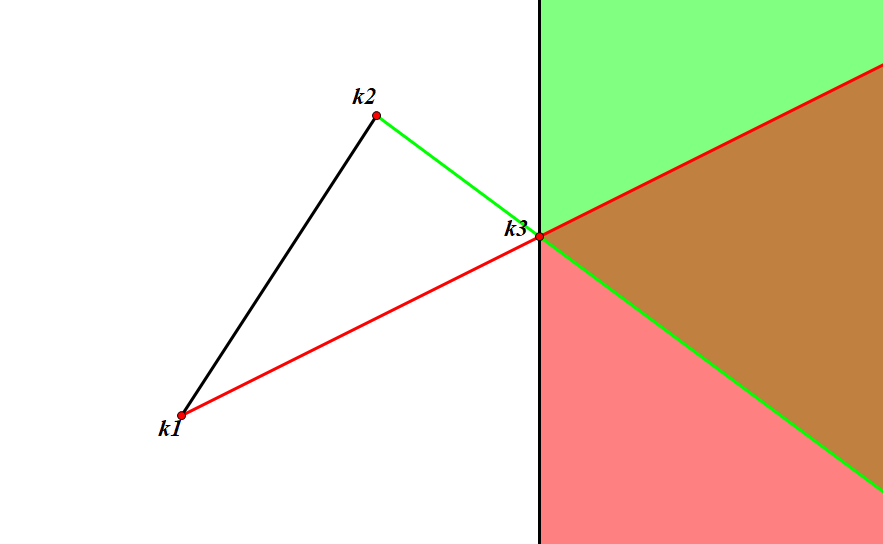
设三个决策点为 ,,,且它们大小递增, 的斜率大于 的斜率。

那么,考虑上图的情况,如果
位于如图所示绿色线以上的部分,有 优于 ;而对于如图所示红色线以下的部分,有
优于 。因此,
在任意的情况下都不是最优点,可以直接舍去。对于其他非上图情况也都可以通过类似的分析发现,只要满足
的斜率大于 的斜率,那么 在任意的情况下都不是最优点。

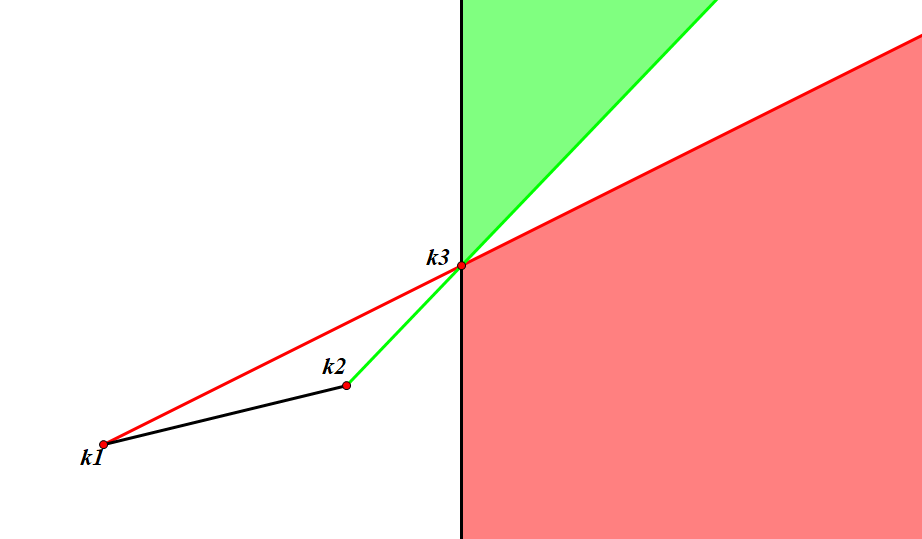
而对于相反的情况,即
的斜率小于
的斜率,注意到红色部分和绿色部分的中间会有间隙,这意味着 并不一定不是最优解,此时 需要保留。
那么,哪个决策点是最优的呢?

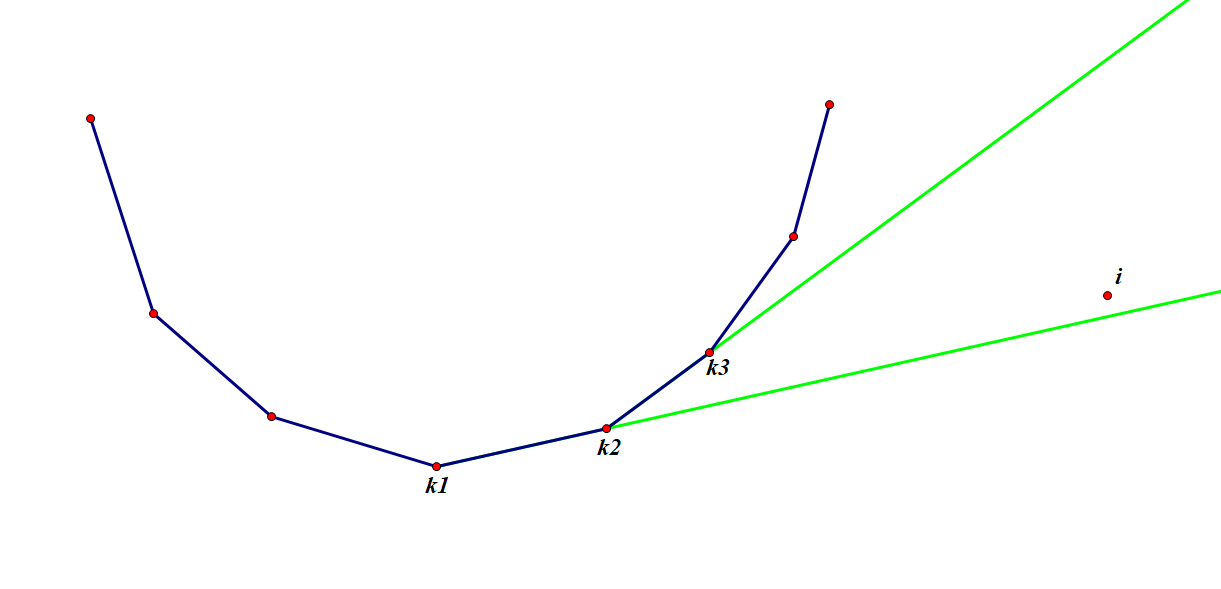
对于一个决策点而言,如果它右侧线段的延长线在
之上,那么它会优于它右侧的下一个决策点;否则它右侧的下一个决策点优于它。考虑上图,我们找到第一个决策点使得它右侧的线段延长线在
点之上,即其右侧线段斜率大于其与
点连线的斜率,那么这个点就是最优决策点。如上图中的 。这是因为
比左侧所有点都要优,也比右侧所有点都要优。
至此,我们已经可以发现:这与常规斜率优化完全类似。维护一个下凸壳即可,二分进行决策选取,时间复杂度成功优化至
。
但是显然还是过不去。能否砍掉二分复杂度?
终极优化
接下来是神的领域
引理3:对于决策点 ,如果满足 ,且
在某一次的转移中较劣,在之后的转移中一定也都是较劣的。
证明:设在转移至 的情况下, 比 优。接下来,让我们来讨论转移至
的情况。根据我们设出的条件,有以下结论: 设左边为
,右边为 ,条件相当于给出 。考虑转移至 的情况,即我们需要证明:
其中 。又因为操作顺序是从小到大,所以一定有
。至此,只需证: 注意到:
所以原式得证,证毕。
根据引理3,由于队首的元素都满足引理3,所以我们可以每次转移答案时将较劣的决策点从队首弹出,保证每一个决策点都最多入队出队各一次。至此,复杂度成功优化至
,完结撒花。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<bits/stdc++.h>
using namespace std;
#define LD long double
int n;
LD h1,sum[8005],h[8005],dp[2][8005];
short from[8005][8005];//存是从哪里转移过来
bitset<8005>jump[8005];//表示转移到当前状态是否进行了一次操作
int cnt=0;
int q[10000005],l=25001,r=25000;//手写队列比较方便
bool check(int k,int kn,int o,int i){
if(l==r) return true;
LD x1=k-1,y1=sum[k]-dp[o][k],x2=kn-1,y2=sum[kn]-dp[o][kn],x3=i,y3=sum[i];
return ((y2-y1)/(x2-x1))>((y3-y1)/(x3-x1));
}
Decimal dfs(int x,int k){
Decimal ret=0;
if(k==0) return (Decimal)(double)h1;
if(jump[x][k]) return (dfs(from[x][k],k-1)+(Decimal)(double)(sum[x]-sum[from[x][k]]))/(x-from[x][k]+1);
else return dfs(from[x][k],k);
}
int main(){
int k,p;
LD tmp;
cin>>n>>k>>p;
scanf("%Lf",&h1);
for(int i=1;i<n;i++){
scanf("%Lf",&tmp);
if(tmp>h1) h[++cnt]=tmp;
}
n=cnt;
k=min(k,n);
sort(h+1,h+1+n);
for(int i=1;i<=n;i++) sum[i]=sum[i-1]+h[i];
for(int i=0;i<=n;i++) dp[0][i]=h1;
for(int j=1;j<=k;j++){
l=r;
q[l]=0;
int dif=j&1,lst=1-dif;
for(int i=1;i<=n;i++){
while(l<r){
if(check(q[l],q[l+1],lst,i)) break;
else l++;
}
dp[dif][i]=max(dp[dif][i-1],(dp[lst][q[l]]+sum[i]-sum[q[l]])/(i-q[l]+1));
if(dp[dif][i-1]>(dp[lst][q[l]]+sum[i]-sum[q[l]])/(i-q[l]+1)) from[i][j]=i-1,jump[i][j]=0;
else from[i][j]=q[l],jump[i][j]=1;
while(l<r){
LD x1=q[r-1]-1,y1=sum[q[r-1]]-dp[lst][q[r-1]],x2=q[r]-1,y2=sum[q[r]]-dp[lst][q[r]],x3=i-1,y3=sum[i]-dp[lst][i];
if(((y2-y1)/(x2-x1))>=((y3-y1)/(x3-x1))) r--;
else break;
}
q[++r]=i;
}
}
Decimal ans=dfs(n,k);
cout << ans.to_string(p*6/5) << "\n";
return 0;
}
|